8.4. Taylor Series
Example 8.4.4 (a): Taylor Series
Find the Taylor series centered at c = 0 for
f(x) = x3 + 2x2 + 3x + 4. Then find
Tf(x, 1). Confirm that
Tf(x, 0) = Tf(x, 1) for all x.
To find a Taylor series we need to find
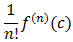 for the given function at
the specified center. First, let's find the various derivatives:
for the given function at
the specified center. First, let's find the various derivatives:
c=0 c=1 f(x) = x3 + 2x2 + 3x + 4 f(0) = 4 f(1) = 10 f '(x) = 3x2 + 4x + 3 f '(0) = 3 f '(1) = 10 f ''(x) = 6x + 4 f ''(0) = 4 f ''(1) = 10 f '''(x) = 6 f '''(0) = 6 f '''(1) = 6 f (n)(x) = 0, n > 3 f (n)(0) = 0 f (n)(1) = 0
Now we can put together the Taylor series, which in this case will reduce to finite polynomials since f (n)(x) = 0 for n > 3:
Tf(x, 0) = 4 + 3/1! x + 4/2! x2 + 6/6! x3 =
= 4 + 3x + 2x2 + x3
In other words, Tf(x, 0) is the original polynomial. For our second Taylor series we get
Tf(x, 1) = 10 + 10/1! (x-1) + 10/2! (x-1)2 + 6/6! (x-1)3 =
= 10 + 10(x-1) + 5(x-1)2 + (x-1)3
But
Tf(x, 1) = 10 + 10(x-1) + 5(x-1)2 + (x-1)3 =so that indeed Tf(x, 0) = Tf(x, 1) for all x.
= 10 + 10x - 10 + 5x2 -10x + 5 + x3 - 3x2 + 3x - 1 =
= 10 - 10 + 5 - 1 + 10x - 10x + 3x + 5x2 - 3x2 + x3 =
= 4 + 3x + 2x2 + x3
 Interactive Real Analysis
Interactive Real Analysis