8.4. Taylor Series
Example 8.4.18 (a): Finding Taylor Series by Definition
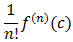 to find the an.
to find the an.
This in theory will always give you the right coefficients, but practically speaking there are two problems: first you need to determine a general formula for the n-th derivative, and second you still need to prove that the series you obtain really converges to the original function.
Example
- Find MacLaurin series for
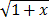
- Guess what the general binomial series for (1+x)a might be.
A MacLaurin series is just a Taylor series centered at c=0. If the function had a Taylor series, the coefficients would be
an =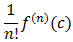
Let's compute the derivatives:
f(x) = (1+x)1/2 f(0) = 1 f '(x) = 1/2 (1+x)1/2 - 1 f '(0) = 1/2 f ''(x) = 1/2(1/2 -1) (1+x)1/2 - 2 f ''(0) = 1/2(1/2 -1) = -1/4 f '''(x) = 1/2(1/2 -1)(1/2 -2) (1+x)1/2 - 3 f '''(0) = 1/2(1/2 -1)(1/2 -2)= 3/8
and so on, so that the general term would be:
for n > 1
This is not that useful (because of the ...) but after some thought we come up with:
f (n)(0) =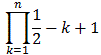
or, since we really need the an we have:
an =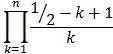
Thus, we claim
=
an xn =

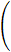
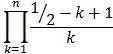
xn
To finish this example we need to show that (a) the power series converges, and (b) it converges to the function. For the radius of convergence we compute, as usual:
r =| an/an+1 | =
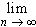
=
| n+1/1/2 - n | = 1
Thus, our series above converges uniformly and absolutely for |x| < 1. But as we know, that does not automatically imply that it converges to our function, so we still need to show that the Taylor or Lagrange remainder goes to zero.
Case 1: 1 > x > 0: Let's take the Lagrange remainder with c=0:
| Rn+1(x) | =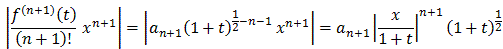
with an as before and t between 0 and x. We also know that 0 < t < x so that:
| Rn+1(x) | < |an+1| xn+1 (1+t)1/2
But we already know that the series
 an xn
converges, so that by the Divergence test
an xn
converges, so that by the Divergence test
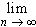 an xn = 0.
But then the remainder must indeed converge to zero.
an xn = 0.
But then the remainder must indeed converge to zero.
Case 2: -1 < x < 0 This time we'll use the regular remainder:
| Rn+1(x) | = 1/n! |(x-t)n f(n+1)(t) dt | =
= 1/n! |(x-t)n (n+1)! an+1(1+t)1/2-n-1 dt | =
= (n+1) | |an+1| |( x-t/1+t )n (1+t)-1/2 dt |

(n+1) | |an+1|
| x-t/1+t |n (1+t)-1/2 dt
with an as before and x < 0. But if we consider the function f(t) = x-t/1+t for x < t < 0 we can take the derivative to see it is monotone decreasing, with maximum value f(x) = 0 on the left side of the interval at t = x. But then the function |f(t)| must have its maximum on the right side at t = 0 with value |f(t)| = |x|. Thus:
| Rn+1(x) |(n+1) | |an+1|
| x-t/1+t |n (1+t)-1/2 dt

(n+1) | |an+1| |x|n
(1+t)-1/2 dt =
= (n+1) | |an+1| |x|n C
for some constant C. As before we can now use the Ratio test to
show that the series
 (n+1) | |an+1| |x|n
converges for |x| < 1 so that by the Divergence test
(n+1) | |an+1| |x|n
converges for |x| < 1 so that by the Divergence test
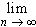 (n+1) | |an+1| |x|n = 0,
which finishes the proof.
(n+1) | |an+1| |x|n = 0,
which finishes the proof.
Some proof !!! But it illustrates nicely the pros and cons of using derivatives to determine the Taylor coefficients.
To take a stab at the general case, recall our answer:
= (1 + x)1/2 =

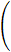
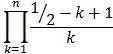
xn
We simply replace 1/2 by a to get the general series for (1 + x)a centered at c = 0:
Theorem: The Binomial Series
The general binomial series for (1+x)a, where a is not an integer, is:(1 + x)a =The series converges uniformly and absolutely for |x| < 1
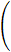
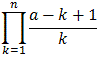
xn
The proof is similar to the special case above ...
 Interactive Real Analysis
Interactive Real Analysis