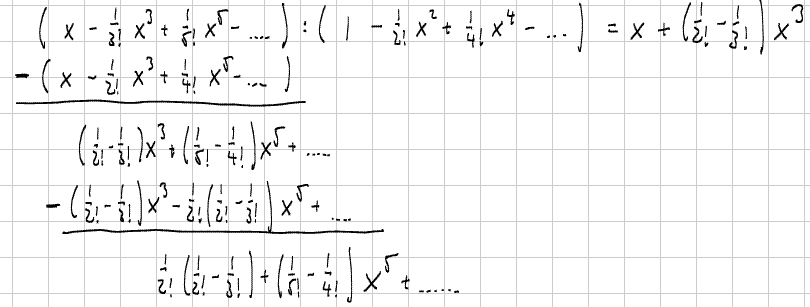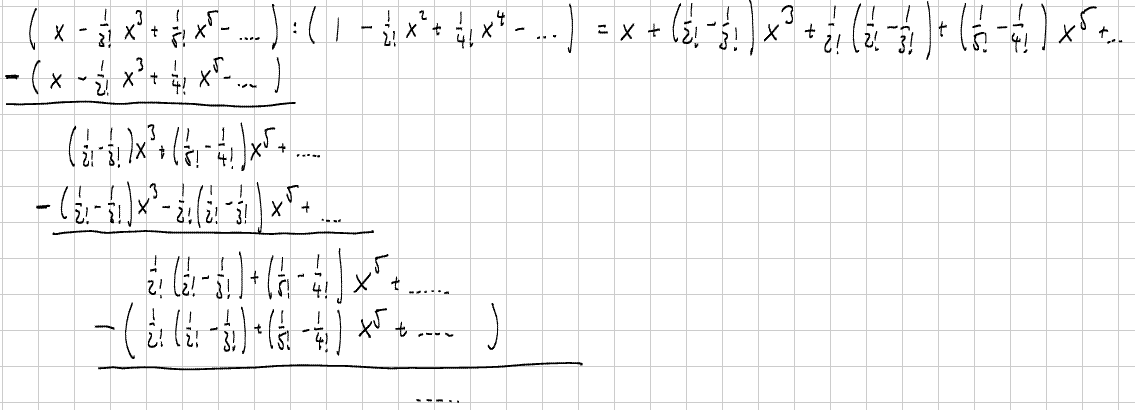8.4. Taylor Series
Example 8.4.18 (f): Finding Taylor Series by Division
Example
- Find the Taylor series centered at zero for f(x) = sin(x)/x.
- Find the first 3 non-zero terms of the Taylor series centered at zero for g(x) = tan(x)
Let's consider the first function f(x) = sin(x)/x. We know the series for the sin function:
sin(x) = x - 1/3! x3 + 1/5! x5 - ... =(-1)n/(2n+1)! x2n+1
Instead of dividing by x we can now multiply through by 1/x
sin(x)/x = 1/x sin(x) =
= 1/x (x - 1/3! x3 + 1/5! x5 - ... ) =
= 1 - 1/3! x2 + 1/5! x4 - ... =
=(-1)n/(2n+1)! x2n
This series representation is valid for all x.
Please note that this works because the constant term a0 of the Taylor series for sin(x) is zero so that the series starts with x. If we divided by, say, x2 the resulting series would not be a Taylor series. In fact, series where positive and negative powers of x are allowed are called Laurent series and are studied extensively in a course on Complex Analysis.
Bonus Question: If you tried to find the series expansion for cos(x)/x, would you get a Taylor series or a Laurent series?
Finally, let's find the series for tan(x), or at least - as requested - the first three terms. Our first impulse might be to take derivatives - let's try that:
f(x) = tan(x) f(0) = 0 a0 = 0 f '(x) = sec2(x) f '(0) = 1 a1 = 1/1! = 1 f ''(x) = 2 sec2(x) tan(x) f ''(0) = 0 a2 = 0 f '''(x) = 2 sec2(x)(2 tan2(x) + sec2(x)) f '''(0) = 2 a3 = 2/3! = 1/3
We found two non-zero terms and we could take one or more derivative to see if the next term works out to be not zero. But taking more derivatives gets more and more complicated, so we'll try a different solution: long division (not necessarily your favorite thing, I know).
Step 0: Since tan(x) = sin(x)/cos(x) and we know the series for both of these trig functions, we start our long division problem by writing:
Step 1: We divide the first term of the first "polynomial" (x) by the first term of the second polynomial (1) to get the first term of the answer (x/1 = x). Then we distribute that term back in, change signs, and add:
Step 2: Now we divide the first term of the resulting "polynomial" ((1/2! - 1/3!)x3) by the first term of the divisor, distribute the answer back in, change signs, and add:
Step 3: One more time gives us the third non-zero coefficient:
Thus, using long division we get as the first few non-zero terms:
- a1 = 1
- a3 = 1/2! - 1/3! = 1/2 - 1/6 = 1/3
- a5 = 1/2!(1/2! - 1/3!) + (1/5! - 1/4!) = 2/15
As an added benefit we can also see that all even coefficients a2k = 0 (and thus also f (2k)(0) = 0). With a little effort you might even be able to see the pattern to determine the general term an ...
To verify our computation, you'll see below the graph of f(x) = tan(x). Click on Options and enter an appropriate 5-th degree polynomial that will best approximate f near x = 0.
 Interactive Real Analysis
Interactive Real Analysis