8.4. Taylor Series
Example 8.4.2 (a): Derivatives of Power Series
Assume that f(x) = e2x has a convergent power series
expression centered at c = 0, i.e.
e2x =
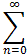 anxn.
Find the coefficients an.
anxn.
Find the coefficients an.
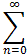 anxn.
Find the coefficients an.
anxn.
Find the coefficients an.
According to our theory we know that if our function can be represented as
e2x =anxn = = a0 + a1x + a2x2 + a3x3 + ...
then
an =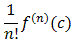
Thus, to find the coefficients an we bascially need to find the n-th derivative of the function f at the center of the series. Taking derivatives on both sides and substituting 0 (the center in this example) we get:
n=0 f(x)=e2x f(0)=1 n=1 f '(x)=2 e2x f '(0)=2 n=2 f ''(x)=22e2x f ''(0)=22 n=3 f (3)(x)=23e2x f (3)(0)=23
and so on, so that by "poor man's induction" we get:
an = 2n/n!
Therefore, if e2x had a series representation, it would have to be:
e2x =2n/n! xn
 Interactive Real Analysis
Interactive Real Analysis