Interactive Real Analysis

• Real Analysis
• 1. Sets and Relations
• 2. Infinity and Induction
• 3. Sequences of Numbers
• 4. Series of Numbers
• 5. Topology
• 6. Limits, Continuity, and Differentiation
• 6.1. Limits
• 6.2. Continuous Functions
• 6.3. Discontinuous Functions
• 6.4. Topology and Continuity
• 6.5. Differentiable Functions
• 6.6. A Function Primer
• 7. The Integral
• 8. Sequences of Functions
• 9. Historical Tidbits
• Java Tools

6.2. Continuous Functions

Illustrating Uniform Continuity:

The examples below try to illustrate uniform continuity. Also, take a look at a Java applet illustrating uniform continuity.

Back

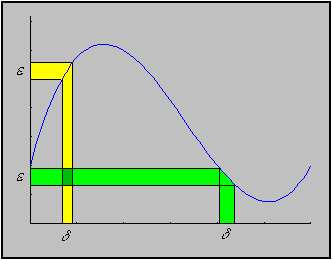
For uniform continuity, there has to be one single that works for a fixed, given . In the picture below that is not possible. If the 'slides' up the positive y-axis, the corresponding must get smaller and smaller. There is no single that will work for any possible location of the interval on the y axis.

Not uniformly continuous

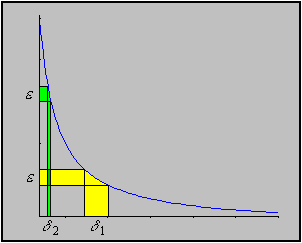
In the example below, however, one can see that regardless of where I place the -interval on the y-axis, it is possible to find one single small that will work for each of those locations of . That is to say, there is one that will work uniformly for all locations of (of course, choosing a smaller means that I am also allowed to pick another, smaller - that will work again uniformly for all -locations).

Is uniformly continuous