6.2. Continuous Functions
Java Applet: Illustrating Uniform Continuity
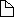
Context
- Click on Options for Control panel
- Select a given epsilon
- Guess a positive delta
- Hit Apply to use new delta
- Slide and zoom using buttons
|
- [+] zoom in and center
- [-] zoom out and center
- [ slide to left
- [<]> slide to right
|
If, for
any given epsilon you can find a positive delta
such that the red area touches the graph always inside the green
area
no matter which part of the graph you are focusing on
then your function is uniformly continuous.
- Click on Options for Control panel
- Select a given epsilon
- Guess a positive delta
- Hit Apply to use new delta
- Slide and zoom using buttons
|
- [+] zoom in and center
- [-] zoom out and center
- [ slide to left
- [<]> slide to right
|
If, for
any given epsilon you can find a positive delta
such that the red area touches the graph always inside the green
area
no matter which part of the graph you are focusing on
then your function is uniformly continuous.
The first function is uniformly continuous, the second function
is continuous, but not uniformly continuous on the real line.
 Compare with regular continuity.
Compare with regular continuity.