1.1. Notation and Set Theory
Proposition 1.1.3: Distributive Law for Sets
Proof:
These relations could be best illustrated by means of a Venn Diagram.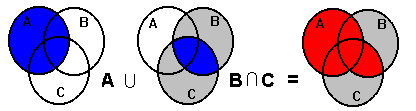
Venn Diagram illustrating A
 (B
(B
 C)
C)
Venn Diagram for (A
 B)
B)
 (A
(A
 C)
C)
Obviously, the two resulting sets are the same, hence �proving' the first law. However, this is not a rigorous proof, and is therefore not acceptable. Here is a �real' proof of the first distribution law:
If x is in A union (B intersect C) then x is either in A or in (B and C). Therefore, we have to consider two cases:
- If x is in A, then x is also in (A union B) as well as in (A union C). Therefore, x is in (A union B) intersect (A union C).
- If x is in (B and C), then x is in
(A union B) because x is in B, and x is
also in (A union C), because x is in C. Hence,
again x is in (A union B) intersect (A union
C). This proves that
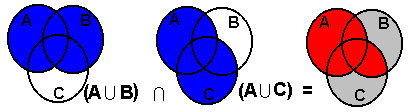
- A
 (B
(B
 C)
C)
 (A
(A
 B)
B)
 (A
(A
 C)
C)
- A
- If x is in A, then x is also in A union (B intersect C).
- If x is in B, then it must also be in C. Hence,
x is in B intersect C, and therefore it is in A
union (B intersect C). That shows that
- A
 (B
(B
 C)
C)
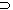 (A
(A
 B)
B)
 (A
(A
 C)
C)
- A
The second distributive laws can be proved the same way, and is left as an exercise.

 Interactive Real Analysis
Interactive Real Analysis