Interactive Real Analysis

• Real Analysis
• 1. Sets and Relations
• 1.1. Notation and Set Theory
• 1.2. Relations and Functions
• 1.3. Equivalence Relations and Classes
• 1.4. Natural Numbers, Integers, and Rational Numbers
• 2. Infinity and Induction
• 3. Sequences of Numbers
• 4. Series of Numbers
• 5. Topology
• 6. Limits, Continuity, and Differentiation
• 7. The Integral
• 8. Sequences of Functions
• 9. Historical Tidbits
• Java Tools

1.4. Natural Numbers, Integers, and Rational Numbers

Example 1.4.5:

Why does one need another number system more complicated than the rational numbers Q?

Back

There are several reasons, many of which are explored in detail in the next chapters. Here are a few of them (which may use terms we are not yet familiar with).

• A simple equation like x² - 9 = 0 does have a solution in Q, but another, just as simple equation x² - 2 = 0 does not have a solution in Q.
• If we construct a right triangle for which two sides have length 1, then we could not measure the length of the remaining side if all we knew were rational numbers.
• We could not measure the circumference of any circle if all we knew were rational numbers.
• If we set x₀ = 2 and then for each integer n > 0 compute the number 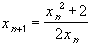successively, then each resulting number is a rational number, the sequence of numbers is getting smaller and smaller, but they seem to get closer and closer to some limit. However, this sequence of numbers does not converge to a rational number. The sequence looks like this (do you know its limit ?):
  • x₀ = 2
  • x₁ = 3/2 = 1.5
  • x₂ = 17/12 = 1.416...,
  • x₃ = 577/408 = 1.414215686 , ...
  • and so on ...
• There are sets consisting of rational numbers that are bounded, but do not have a least upper bound in Q.
• Equations such as sin(x) = 1/2 or cos(x) = 0 do not have solutions in Q.