1.2. Relations and Functions
Examples 1.2.7(b):
Which of the following functions are one-one, onto, or bijections ? The domain
for all functions is R.
- f(x) = 2x + 5
- g(x) = arctan(x)
- g(x) = sin(x)
- h(x) = 2x3 + 5x2 - 7x + 6
1. Linear Function
This function is linear. The equation y = 2x + 5 has a unique solution for every x, so that the function is one-one and onto, i.e. a bijection. In fact, all linear functions are bijections.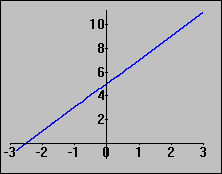 f(x) = 2x + 5 is a bijection.
f(x) = 2x + 5 is a bijection.
2. Inverse Functions
This function is the inverse function of the tangent function. As such, it must be one-to-one. It is onto if the range is [-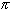 / 2,
/ 2, 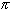 / 2],
but not if the range is R. In fact, all inverse functions are one-to-one.
/ 2],
but not if the range is R. In fact, all inverse functions are one-to-one.
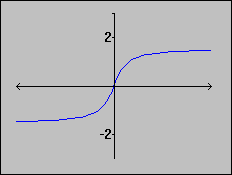 g(x) = arctan(x) is injective,
not surjective on R.
g(x) = arctan(x) is injective,
not surjective on R.
3. Periodic Function
Since this function is periodic, it can not be one-to-one. It is onto, if the range is the interval [-1, 1], but not onto if the range is R. In fact, every periodic function is not one-to-one.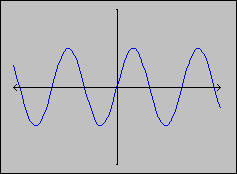 g(x) = sin(x) is neither
one-to-one nor onto R.
g(x) = sin(x) is neither
one-to-one nor onto R.
4. Odd Degree Polynomial
This is an odd-degree polynomial. Hence, the limit as x approaches plus or minus infinity must be plus or minus infinity, respectively. That means that the function is onto. Since most third degree equations have three zero, this function is probably not one-to-one. A look at the graph confirms this. In fact, every odd-degree polynomial is onto while no even degree polynomial is onto.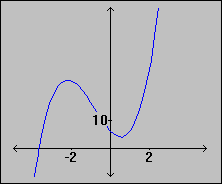 h(x) = 2x3 + 5x2 - 7x + 6
is onto, not one-to-one
h(x) = 2x3 + 5x2 - 7x + 6
is onto, not one-to-one
 Interactive Real Analysis
Interactive Real Analysis