1.4. Natural Numbers, Integers, and Rational Numbers
Examples 1.4.3(a):
Let A be the set N x N and define an equivalence relation r on N x N and
addition of the equivalence classes as follows:
The elements in the equivalence class of [(1, 2)] are all numbers (x,y)
that are related to (1, 2), i.e. all (x,y) such that
- (a,b) is related to (a',b') if a + b' = a' + b
- [(a,b)] + [(a',b')] = [(a + a', b + b')]
- [(a,b)] * [(a', b')] = [(a * b' + b * a', a * a' + b * b')]
- 1 + y = x + 2 or
- y - x = 1
- (2, 3), (3, 4), (100, 101)
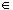 [(1, 2)]
[(1, 2)]
- (x, y)
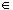 [(0, 0)] if
(0, 0) ~ (x,y)
[(0, 0)] if
(0, 0) ~ (x,y)
- 0 + y = x + 0 or y = x
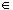 [(0, 0)]
[(0, 0)]
- (x, y)
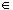 (1, 0) if
(1, 0) ~ (x, y)
(1, 0) if
(1, 0) ~ (x, y)
- 1 + y = 0 + x or x - y = 1
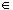 [(1, 0)]. To determine which of the pairs (1, 5), (5, 1), (10, 14), (7, 3)
are in the same equivalence classes, all we have to do is compare the
differences between the second and the first entry:
[(1, 0)]. To determine which of the pairs (1, 5), (5, 1), (10, 14), (7, 3)
are in the same equivalence classes, all we have to do is compare the
differences between the second and the first entry:
- (1,5): the difference y - x = 4
- (5, 1): the difference y - x = -4
- (10, 14): the difference y - x = 4
- (7, 3): the difference y - x = -4
 Interactive Real Analysis
Interactive Real Analysis