6.5. Differentiable Functions
Definition 6.5.11: Local Extremum
Let f be a function defined on a domain
D, and c a point in D.
- If there exists a neighborhood U of
c with f(c)
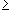 f(x)
for all x in U, then f(c) is
called a local maximum for the function f
that occurs at x = c.
f(x)
for all x in U, then f(c) is
called a local maximum for the function f
that occurs at x = c.
- If there exists a neighborhood U of
c with f(c)
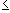 f(x) for all x in
U, then f(c) is called a local minimum for the
function f that occurs at x = c.
f(x) for all x in
U, then f(c) is called a local minimum for the
function f that occurs at x = c.
- If f(x) has either a local minimum or a local maximum at x = c, then f(c) is called local extremum of the function f.
 Interactive Real Analysis
Interactive Real Analysis