6.2. Continuous Functions
Definition 6.2.2: Continuity
A function is continuous at a point c in its
domain D if: given any  > 0 there exists a
> 0 there exists a
 > 0 such that if
x
> 0 such that if
x 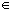 D and
| x - c | <
D and
| x - c | <  then
| f(x) - f(c) | <
then
| f(x) - f(c) | <  .
.
 > 0 there exists a
> 0 there exists a
 > 0 such that if
x
> 0 such that if
x 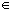 D and
| x - c | <
D and
| x - c | <  then
| f(x) - f(c) | <
then
| f(x) - f(c) | <  .
.
A function is continuous in its domain D if it is continuous at every point of its domain.
![]() This, like many epsilon-delta definitions and arguments, is
not easy to understand. Click on the Java icon to see an
applet that tries to illustrate the definition.
This, like many epsilon-delta definitions and arguments, is
not easy to understand. Click on the Java icon to see an
applet that tries to illustrate the definition.
 Interactive Real Analysis
Interactive Real Analysis