Interactive Real Analysis

• Real Analysis
• 1. Sets and Relations
• 2. Infinity and Induction
• 3. Sequences of Numbers
• 4. Series of Numbers
• 5. Topology
• 6. Limits, Continuity, and Differentiation
• 6.1. Limits
• 6.2. Continuous Functions
• 6.3. Discontinuous Functions
• 6.4. Topology and Continuity
• 6.5. Differentiable Functions
• 6.6. A Function Primer
• 7. The Integral
• 8. Sequences of Functions
• 9. Historical Tidbits
• Java Tools

6.1. Limits

Example 6.1.1:

Consider the function f, where f(x) = 1 if x 0 and f(x) = 2 if x > 0.

1. The sequence {1/n} converges to 0. What happens to the sequence { f( 1/n ) } ?
2. The sequence { 3 + (-1)ⁿ} is divergent. What happens to the sequence { f(3 + (-1)ⁿ)} ?
3. The sequence {(-1)ⁿ / n } converges to zero. What happens to the sequence { f((-1)ⁿ / n ) } ?

Back

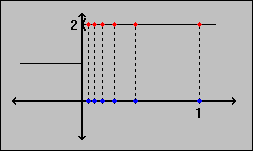
1. For the first sequence, we clearly have that f(1/n) = 2 for all n. Hence, the limit of f(1/n) equals 2. So a function applied to a sequence results in a new sequence that can converge to a different number.
2. For the second sequence, we know that 3 + (-1)ⁿ > 0 for all n. Hence, f(3 + (-1)ⁿ) = 2 for all n. This time, a function applied to a divergent sequence results in a convergent one.
3. For the third sequence we know that alternating terms switch signs. Hence, f((-1)ⁿ / n) = 1 if n is odd, and 2 if n is even. But then the resulting new sequence is divergent. Hence, we have an example where a function can turn a convergent sequence into a divergent one.