6.2. Continuous Functions
Example 6.2.1:
Which of the two functions is intuitively continuous and which
one is not ?
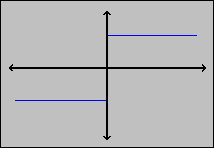
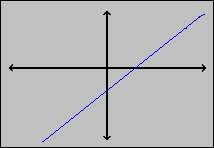
Since Descartes claims that a function is continuous if its graph
can be drawn without lifting the pencil, we will look at the graph
of each function:
- f(x) = 1 if x > 0 and f(x) = -1 if x < 0. Is this function continuous ?
- f(x) = 5x - 6. Is this function continuous?
 Interactive Real Analysis
Interactive Real Analysis