6.3. Discontinuous Functions
Examples 6.3.4(d):
What kind of discontinuity does the function
g(x) have at every point (with proof).
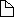
Back
This function is impossible to graph. The picture above is only
a poor representation of the true graph. Nonetheless, take an
arbitrary point
x0 on the real axis. We can find
a sequence
{xn} of rational points that converge to
x0 from the right. Then
g(xn) converges to
1. But we can also find a
sequence
{xn} of irrational points converging to
x0 from the right. In that case
g(xn) converges to
0. But that means that the limit
of
g(x) as
x approaches
x0 from the right
does not exist. The same argument, of course, works to show that the limit of
g(x) as
x approaches
x0 from
the left does not exist. Hence,
x0 is
an essential discontinuity for
g(x).