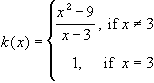6.3. Discontinuous Functions
Examples 6.3.4(a):
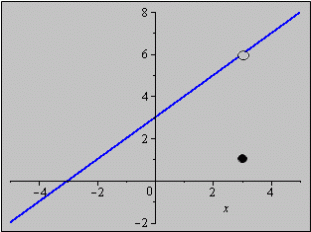
We can easily check (by factoring the numerator) that the limit as x approaches 3 from the right and from the left is equal to 6. Hence, the limit as x approaches 3 exists, and therefore the function has a removable discontinuity at x = 3. If we define k(3) = 6 instead of k(3) = 1 then the function, in fact, will be continuous on the real line.
 Interactive Real Analysis
Interactive Real Analysis