6.2. Continuous Functions
Example 6.2.8(a):
It helps to look at the graph of the function: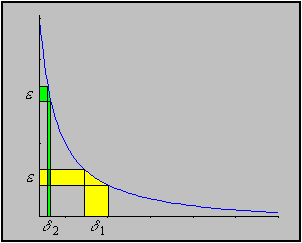
 -
interval 'slides' up the positive y-axis, the corresponding
-
interval 'slides' up the positive y-axis, the corresponding
 -interval
on the x-axis gets smaller and smaller. That indicates that the
function is not uniformly continuous - but it is of course
not a proof. So:
-interval
on the x-axis gets smaller and smaller. That indicates that the
function is not uniformly continuous - but it is of course
not a proof. So:
Take any  = 1. Does there exist
any
= 1. Does there exist
any  such that
such that
if | t - s | <then | f(t) - f(s) | <
= 1 ?
The basic idea is easy: since | f(t) - f(s) | = | 1/t - 1/s | = | s - t | * 1 / | st |,
we can see that this might approach infinity if s and t approach
zero, and therefore will be bigger than any chosen  .
All we have to do now is formalize this proof.
.
All we have to do now is formalize this proof.
Assume there exists such a  .
Without loss of generality we may assume that
.
Without loss of generality we may assume that
 < 1 (why ?). Then let
s = t +
< 1 (why ?). Then let
s = t +  / 2
and set
t =
/ 2
and set
t =  / 2.
We have (assuming that s, t are positive):
/ 2.
We have (assuming that s, t are positive):
| f(t) - f(s) | = | 1/s - 1/t | = | (t - s) / st | => 1
But now, no matter what  < 1 is we can
make | f(t) - f(s) | > 1. Therefore, the function is not uniformly continuous.
< 1 is we can
make | f(t) - f(s) | > 1. Therefore, the function is not uniformly continuous.
This proof, loosely speaking, depends on the fact that after simplification | f(t) - f(s) | goes to infinity if s and t approach zero. That is exactly the situation as described in the above picture.
 Interactive Real Analysis
Interactive Real Analysis