6.4. Topology and Continuity
Examples 6.4.9(b):
Using a computer it is simple enough to draw this function and to see the approximate solution. However, it is even easier to prove that there must be a solution (without specifying where the solution would be).The function p(x) is an odd-degree polynomial. Therefore:
- If c =
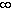 ,
then
,
then 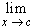 p(x) =
p(x) = 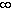 ,
so that there exists A such that p(A) > 0
,
so that there exists A such that p(A) > 0
- If c = -
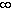 ,
then
,
then 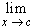 p(x) = -
p(x) = - 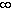 ,
so that there exists B such that p(B) < 0
,
so that there exists B such that p(B) < 0
Hence, by Bolzano's theorem there exists a zero of p(x) between the (unknown !) numbers A and B.
 Interactive Real Analysis
Interactive Real Analysis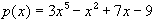 = 0
has at least one solution in R
= 0
has at least one solution in R