6.4. Topology and Continuity
Examples 6.4.9(a):
Let's take a look at the two function f(x) = cos(x) and g(x) = x in one coordinate system: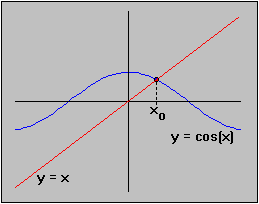
h(-Hence, by Bolzano's theorem there must be at least one place x0 where h( x0) = 0, or equivalently where cos( x0) = x0.) = -1 +
> 0
h() = -1 -
< 0
One can use Bolzano's theorem to construct an algorithm that will find zeros of a function to a prescribed degree of accuracy in many cases. In simple terms:
- start with an interval [a, b] where h(a) * h(b) < 0 (i.e. h(a) and h(b) have opposite signs)
- find a point c - usually (a + b) / 2 - such that either
h(a) * h(c) < 0 or h(b) * h(c) < 0
- if h(a) * h(c) < 0, repeat this procedure with b replaced by c
- if h(b) * h(c) < 0, repeat this procedure with a replaced by c.
- Continue until the difference b - a is small enough.
Would this procedure find the zero of the function f(x) = x2 in the interval [-1, 1] ?
 Interactive Real Analysis
Interactive Real Analysis