5.1. Open and Closed Sets
Proposition 5.1.3: Unions of Open Sets, Intersections of Closed Sets
- Every union of open sets is again open.
- Every intersection of closed sets is again closed.
- Every finite intersection of open sets is again open
- Every finite union of closed sets is again closed.
Proof:
Let { U n } be a collection of open sets, and let U = U n.
Take any x in U. Being in the union of all U's,
it must be contained in one specific
U n. Since that set is open, there exists a
neighborhood of x contained in that specific
U n.
But then that neighborhood must also be contained in the union
U. Hence, any x in U has a neighborhood that is
also in U, which means by definition that U is
open.
U n.
Take any x in U. Being in the union of all U's,
it must be contained in one specific
U n. Since that set is open, there exists a
neighborhood of x contained in that specific
U n.
But then that neighborhood must also be contained in the union
U. Hence, any x in U has a neighborhood that is
also in U, which means by definition that U is
open.
To prove the second statement, simply use the definition of closed sets and de Morgan's laws.
Now let U n, n=1, 2, 3, ..., N be finitely many open sets. Take x in the intersection of all of them. Then:
- x is in the first set: there exists an
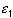 with
( x -
with
( x - 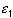 ,
x +
,
x + 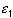 )
contained in the first set
)
contained in the first set
- x is in the second set: there is
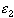 with
( x -
with
( x - 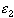 ,
x +
,
x + 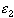 )
contained in the second set.
)
contained in the second set.
- ....
- x is in the N-th set: there is
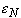 with
( x -
with
( x - 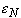 ,
x +
,
x + 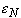 )
contained in the last set.
)
contained in the last set.
- let
 =
min{
=
min{ 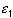 ,
,
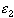 , ...,
, ...,
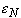 }.
Then
( x -
}.
Then
( x -  ,
x +
,
x +  )
is contained in each set U n
)
is contained in each set U n
The last statement follows again from de Morgan's laws.

 Interactive Real Analysis
Interactive Real Analysis