5.2. Compact and Perfect Sets

Theorem 5.2.6: Heine-Borel Theorem

A set S of real numbers is compact if and only if every open cover C of S can be reduced to a finite subcovering.

Proof:

First, assume that every open cover C of S can be reduced to a finite subcovering. We will show that S must then be closed and bounded, which means by the previous result that S is compact.

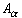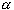
S must be bounded: Take the collection C = { : S}, where 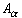= ( 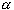- 1, 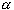+ 1). Then this collection is an open cover of S, and by assumption can be reduced to a finite subcovering of S. But if aj1 is the smallest of the centers of the sets 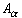, and aj2 is the largest one, then S is contained in the set ( aj1 - 1, aj2 + 1) and is therefore bounded.

S must be closed: Suppose S was not closed. Then there exists an accumulation point s of S that is not contained in S. Since s is an accumulation point of S we know:

because every neighborhood of s must contain elements from S. The sequence { an } clearly converges to s. Define the collection of sets Then each set in C is open, being the complement of closed sets. They also cover S, because the only point that this collection is missing is the point s, which is not part of S. By assumption, a finite subcover already covers S. If N is the largest index of that finite subcovering, then aN+1 is not part of that subcovering. However, aN+1 is an element of S, so that this subcovering can not cover S. That is a contradiction, showing that if S was not closed, not every covering of S can be reduced to a finite subcovering. Hence, S must be closed.

Now we have to prove the other direction. Assume therefore that S compact. Let C be any open cover of S. We need to reduce C to a finite subcover. Since S is compact, we know it is closed and bounded. Then a = inf(S) and b = sup(S) are both part of S ( Why ?). Define the set A as

Then the set A is not empty (because a A). Define Since A is a subset of [a, b], we know that a < c b. Suppose c < b. Since S is closed, comp(S) is open. Therefore, if c comp(S) then there exists an open neighborhood U of c that is contained in [a, b] (because c < b) and disjoint from S. But then c can not be the supremum of the set A. Therefore, if c < b then c S. Then c must be contained in some set 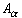from the open cover C of S. Choose two points y and z in 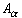with y < c < z. As before, there exists a finite subcollection of C whose members cover [a, y] S. Then these sets, together with 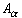cover [a, z] S. But then z A, which means again that c can not be the upper bound for A. This means that assuming c < b leads to a contradiction, so that c = b. But that will be exactly what we need. If sup(A) = c = b, then let 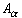be that member of the open cover C that contains b. There exists some open neighborhood (b - , b + ) contained in 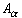. But b - is not an upper bound for A, so there exists x with x > b - and x A. Then [a, x] S is covered by a finite number of members of C. Together with the set 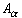these sets form a finite open cover for S.

We have indeed reduced the open cover of S to a finite subcovering of S, finishing the proof. I think.

Next | Previous | Glossary | Map