5.2. Compact and Perfect Sets
Proposition 5.2.3: Compact means Closed and Bounded
Proof:
First, suppose S is closed and bounded. Take a sequence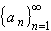 in S.
Because S is bounded, the sequence is bounded also, and by
the Bolzano-Weierstrass theorem we can extract a convergent
subsequence from
in S.
Because S is bounded, the sequence is bounded also, and by
the Bolzano-Weierstrass theorem we can extract a convergent
subsequence from
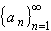 .
Using the theorem about closed sets, accumulation points and
sequences, we know that the limit of the subsequence is again in
S. Hence, S is compact.
.
Using the theorem about closed sets, accumulation points and
sequences, we know that the limit of the subsequence is again in
S. Hence, S is compact.
Now assume that S is compact. We have to show that S is bounded and closed.
Suppose S was not bounded. Then for every n there
exists a number
a n  S
with
| a n | > n. But then no subsequence of the
sequence
S
with
| a n | > n. But then no subsequence of the
sequence
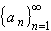 will converge
to a finite number, hence S can not be compact. Thus,
S must be bounded.
will converge
to a finite number, hence S can not be compact. Thus,
S must be bounded.
Suppose S was not closed. Then there exists an accumulation
point c for the set S that is not contained in S.
Since c is an accumulation point, there exists a sequence
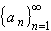 of elements
in S that converges to c. But then every subsequence
of that sequence will also converge to c, and since c
is not in S, that contradicts compactness. Hence, S
must be closed.
of elements
in S that converges to c. But then every subsequence
of that sequence will also converge to c, and since c
is not in S, that contradicts compactness. Hence, S
must be closed.

 Interactive Real Analysis
Interactive Real Analysis