Topology: Problems
1. Let S be any subset of the real numbers. Prove that int(S) is open. Prove that
S is open if and only if S = int(S).
2. Let S be any subset of real numbers. Define the closure of the set S as cl(S)
= S 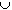 bd(S). Prove that cl(S) is a closed
set.
bd(S). Prove that cl(S) is a closed
set.
3. Let K be a compact set and U an open set containing K. Prove that there
exists an  > 0 such that if k
> 0 such that if k 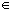 K then the interval (k -
K then the interval (k -  , k +
, k +  ) is contained in U.
) is contained in U.
4. Prove that every closed subset of a compact set is compact.
5. Let S be any subset of real numbers. Call a set robust if it is equal to the closure of its interior.
Then
- Is every open set robust ? Is every closed set robust ?
- Is every robust set open ? Is every robust set closed ?
- Is every closed interval robust ? Is every robust set equal to a closed interval ?
- Make a conjecture to characterize all robust sets in the real line.
6. Let  ,
,  , ... be perfect sets
and suppose that
, ... be perfect sets
and suppose that 
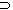

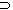
 .. Is the intersection of all
.. Is the intersection of all  perfect ?
perfect ?
7. Give an example of non-empty, closed sets 
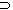

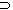
 ... such that their intersection is empty.
... such that their intersection is empty.
8. Give an example of non-empty, closed sets 



 ... such that their union is open.
... such that their union is open.
9. Give an example of open sets 
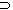

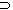
 ... such that their union is closed and non-empty
... such that their union is closed and non-empty
10. Give an example of a totally disconnected subset S of the interval [0, 1] such that the closure
cl(S) = [0, 1].
11. What is the interior of the Cantor set ? What is the boundary of the Cantor set ?
12. Write the real line as the union of two totally disconnected sets.
13. Let  ,
,  ,
,  , ... be closed sets such that their union is equal to the real line. Prove that at least
one of the sets
, ... be closed sets such that their union is equal to the real line. Prove that at least
one of the sets  must have non-empty interior. (Hint: Look at the
proof that perfect sets are uncountable).
must have non-empty interior. (Hint: Look at the
proof that perfect sets are uncountable).
(bgw)
 ,
,  , ... be perfect sets
and suppose that
, ... be perfect sets
and suppose that 

 .. Is the intersection of all
.. Is the intersection of all  perfect ?
perfect ?

 ... such that their intersection is empty.
... such that their intersection is empty.

 ... such that their union is open.
... such that their union is open.

 ... such that their union is closed and non-empty
... such that their union is closed and non-empty ,
,  ,
,  , ... be closed sets such that their union is equal to the real line. Prove that at least
one of the sets
, ... be closed sets such that their union is equal to the real line. Prove that at least
one of the sets  must have non-empty interior. (Hint: Look at the
proof that perfect sets are uncountable).
must have non-empty interior. (Hint: Look at the
proof that perfect sets are uncountable).