5.1. Open and Closed Sets
Examples 5.1.2(c):
Are the sets
{1, 1/2, 1/3, 1/4, 1/5, ...} and
{1, 1/2, 1/3, 1/4, ...} 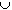 {0}
open, closed, both, or neither ?
{0}
open, closed, both, or neither ?
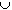 {0}
open, closed, both, or neither ?
{0}
open, closed, both, or neither ?
- The set {1, 1/2, 1/3, 1/4, 1/5, ... } is not open, because it does not contain any neighborhood of the point x = 1.
- The complement of the set {1, 1/2, 1/3, 1/4, 1/5, ... } contains the number 0. But if (-a, a) is any neighborhood of 0, then there exists an N so large such that 1/N < a. This neighborhood is not part of the complement, because it contains the element 1/N from the set. Therefore the complement is not open. That means, however, that the original set is not closed.
- The set
{1, 1/2, 1/3, 1/4, 1/5, ... }
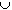 {0}
is not open because it does not contain any neighborhood of the point
x = 1.
{0}
is not open because it does not contain any neighborhood of the point
x = 1.
- For the last question, we need to look at the complement of
the set
{1, 1/2, 1/3, 1/4, 1/5, ... }
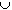 {0}:
{0}:
- comp( {1, 1/2, 1/3, 1/4, 1/5, ... }
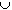 {0} ) =
{0} ) =
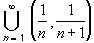
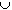 (1,
(1, 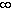 )
) 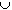 (-
(-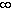 , 0)
, 0)
- comp( {1, 1/2, 1/3, 1/4, 1/5, ... }
 Interactive Real Analysis
Interactive Real Analysis