4.2. Convergence Tests
Root Test
Consider the series 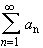 . Then:
. Then:
Compare this test with the Ratio test. Although
this root test is more difficult to apply, it is better than the ratio
test in the following sense: there are series for which the ratio test give
no information, yet the root test will be conclusive. You can also use the
root test to prove the ratio test , but not visa versa.
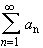 . Then:
. Then:
- if lim sup | a n | 1/n < 1 then the series converges absolutely
- if lim sup | a n | 1/n > 1 then the series diverges
- if lim sup | a n | 1/n = 1, this test gives no information
It is important to remember that when the root test gives 1 as the answer for the lim sup, then no conclusion at all is possible.
The use of the lim sup rather than the regular limit has the advantage that we do not have to be concerned with the existence of a limit. On the other hand, if the regular limit exists, it is the same as the lim sup, so that we are not giving up anything using the lim sup.
Proof:
Assume that
lim sup | a n | 1/n < 1:
Because of the properties of the limit superior, we know that there exists
 > 0 and
N > 1 such that
> 0 and
N > 1 such that
| a n | 1/n < 1 -for n > N. Raising both sides to the n-th power we have:
| a n | < (1 -for n > N. But the terms on the right hand side form a convergent geometric series. Hence, by the comparison test the series with terms on the left-hand side will converge absolutely.) n
The proof for the second case if left as an exercise.
 Interactive Real Analysis
Interactive Real Analysis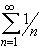 ?
Does the series converge or diverge ?
?
Does the series converge or diverge ?
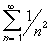 ?
Does the series converge or diverge ?
?
Does the series converge or diverge ?
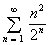 converge or diverge ?
converge or diverge ?