4.2. Convergence Tests
Alternating Series Test
A series of the form
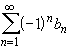 with
b n
with
b n  0
is called Alternating Series. If the sequence
0
is called Alternating Series. If the sequence
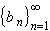 is decreasing and converges to zero, then the sum converges.
is decreasing and converges to zero, then the sum converges.
This test does not prove absolute convergence. In fact, when checking
for absolute convergence the term 'alternating series' is meaningless.
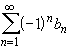 with
b n
with
b n  0
is called Alternating Series. If the sequence
0
is called Alternating Series. If the sequence
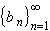 is decreasing and converges to zero, then the sum converges.
is decreasing and converges to zero, then the sum converges.
It is important that the series truly alternates, that is each positive term is followed by a negative one, and visa versa. If that is not the case, the alternating series test does not apply (while Abel's Test may still work).
Proof:
Let a n = (-1) n. Then the formal sum
 has bounded partial sums (although the sum does not itself converge.
Why not ?). Then, with the given choice of
has bounded partial sums (although the sum does not itself converge.
Why not ?). Then, with the given choice of
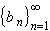 Abel's test applies directly, showing that the series indeed converges.
Abel's test applies directly, showing that the series indeed converges.

 Interactive Real Analysis
Interactive Real Analysis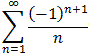 converge or diverge ?
converge or diverge ?
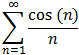 ?
?