4.1. Series and Convergence
Theorem 4.1.6: Absolute Convergence and Rearrangement
Let
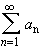 be an absolutely convergent series. Then any rearrangement of
terms in that series results in a new series that is also
absolutely convergent to the same limit.
be an absolutely convergent series. Then any rearrangement of
terms in that series results in a new series that is also
absolutely convergent to the same limit.
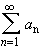 be an absolutely convergent series. Then any rearrangement of
terms in that series results in a new series that is also
absolutely convergent to the same limit.
be an absolutely convergent series. Then any rearrangement of
terms in that series results in a new series that is also
absolutely convergent to the same limit.
Let
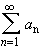 be a conditionally convergent series. Then, for any real
number c there is a rearrangement of the series such
that the new resulting series will converge to c.
be a conditionally convergent series. Then, for any real
number c there is a rearrangement of the series such
that the new resulting series will converge to c.
Proof:
Suppose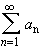 is
absolutely convergent. Then the sequence
is
absolutely convergent. Then the sequence
Sn = |a1| + |a2| + ... + | an|converges. In particular, it is bounded, i.e. |Sn| < K for some number K. If we take any rearrangement of terms in the series and form a new sequence of partial sums:
Tn = |then Tn is again bounded by the same number K. But since all terms in the partial sum Tn are positive the sequence is monotone increasing. Therefore {Tn} is monotone increasing and bounded and must therefore converge.| + |
| + ... |
|
It remains to show that the limit of the rearrangement is the same as the limit of the original series. That is left as an exercise.
Finally suppose the series 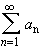 converges conditionally. Let's first collect a few facts:
converges conditionally. Let's first collect a few facts:
- By the divergence test (which we will prove later) we know that the sequence of general terms an converges to zero.
- The series does not converge absolutely.
- Since the sequence of partial sums of absolute values is increasing it means that the series of absolute values must "converge" to positive infinity.
- There must be infinitely many positive terms among the aj. If we call them bj and collect them to form a series then that new series must "converge" to positive infinity (why?).
- There must be infinitely many negative terms among the aj. If we call them cj and collect them to form a series then that new series must "converge" to negative infinity (why?).
- Collect enough bj so that they add up to a number just bigger than c
- Add as many terms from cj as is necessary to make the resulting sum just less than c
- Add again terms from bj to be just bigger than c, then again terms from cj to be less than c, and so on.
Then you can show that the resulting arrangment of bj's and cj indeed forms a series that converges to c. As usual, the details of this proof are left as an exercise.

 Interactive Real Analysis
Interactive Real Analysis