4.3. Special Series
Definition: Harmonic Series
The series
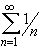 = 1 + 1/2 + 1/3 + 1/4 + 1/5 + ... is called harmonic series. It
diverges to infinity.
= 1 + 1/2 + 1/3 + 1/4 + 1/5 + ... is called harmonic series. It
diverges to infinity.
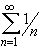 = 1 + 1/2 + 1/3 + 1/4 + 1/5 + ... is called harmonic series. It
diverges to infinity.
= 1 + 1/2 + 1/3 + 1/4 + 1/5 + ... is called harmonic series. It
diverges to infinity.
For an interesting application of the harmonic series, check the story about the Leaning Tower of Lire.
Proof:
We need to estimate the n-th term in the sequence of partial sums.S N = 1 + 1/2 + 1/3 + 1/4 + ... + 1/nNow consider the following subsequence extracted from the sequence of partial sums:
S 1 = 1
S 2 = 1 + 1/2
S 4 = 1 + 1/2 + (1/3 + 1/4)
1 + 1/2 + (1/4 + 1/4) = 1 + 1/2 + 1/2 = 1 + 2/2
S 8 = 1 + 1/2 + (1/3 + 1/4) + (1/5 + 1/6 + 1/7 + 1/8)In general, one can use induction (do it as an exercise) to show that
1 + 1/2 + (1/4 + 1/4) + (1/8 + 1/8 + 1/8 + 1/8) = 1 + 1/2 + 1/2 + 1/2 = 1 + 3/2
S 2 kfor all k. Hence, the subsequence { S 2 k } extracted from the sequence of partial sums { S N } is unbounded. But then the sequence { S N } can not converge either and must diverge to infinity.1 + k / 2

 Interactive Real Analysis
Interactive Real Analysis