4.3. Special Series
Definition: Alternating Harmonic Series
The series
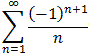 is called the Alternating Harmonic series. It converges but
not absolutely, i.e. it converges conditionally.
is called the Alternating Harmonic series. It converges but
not absolutely, i.e. it converges conditionally.
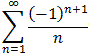 is called the Alternating Harmonic series. It converges but
not absolutely, i.e. it converges conditionally.
is called the Alternating Harmonic series. It converges but
not absolutely, i.e. it converges conditionally.
Proof:
We already know that the series of absolute values does not converge by a previous example. Hence, the series does not converge absolutely. As for regular convergence, consider the following two partial sums:
and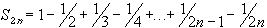
We have that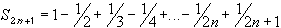
S 2n+2 - S 2n = 1 / (2n+1) - 1 / (2n+2) > 0and
S 2n+3 - S 2n+1 = - 1 / (2n+2) + 1/ (2n+3) < 0which means for the two subsequences
{ S 2n } is monotone increasing and { S 2n+1 } is monotone decreasingFor each sequence we can combine pairs to see that
S 2nfor all n. Hence, both subsequences are monotone and bounded and must therefore be convergent. Define their limits as1 and S 2n+1
0
lim S 2n = L and lim S 2n+1 = MThen
| M - L | = | lim (S 2n+1 - S 2n) | = 1 / (2n+1)which converges to zero. Therefore, M = L, i.e. both subsequences converge to the same limit. But this common limit is the same as the limit of the full sequence, because: given any
 > 0 we have
> 0 we have
- there exists an integer N such that
| L - S 2n | <
 if n > N
if n > N
- there exists an integer M such that
| L - S 2n+1 | <
 if n > M
if n > M
 > 0 we have
> 0 we have
| L - S n | <for n > K because n is either even or odd. Hence, the alternating harmonic series converges conditionally.

 Interactive Real Analysis
Interactive Real Analysis