Ratio Test
Examples 4.2.16(d):
Here is an alternative proof of the ratio test that uses the root
test directly. Note that this shows that the root test is 'better' than
the ratio test, because the ratio test can be deduced from the root test.
Proof:
First, recall the ratio testif lim sup | a n+1 / a n | < 1 then the series converges absolutely.and the root test
if lim sup | a n | 1/n < 1 then the series converges absolutely.We will use the root test to prove the ratio test
Assume that lim sup | a n+1 / a n | < 1. Using the properties of the limit superior, there exists a number c with 0 < c < 1, such that
| a n+1 / a n | < cfor n > N or equivalently,
| a n+1 | < c | a n |for n > N. Then, for any positive integer k, we have that:
| a N+k |for all k > 1. Making the substitution N + k = n, for n > N, this is equivalent to:c | a N+k-1 |
c ( c | a N+k-2 |)
...
c k |a N |
| a n |orc n-N | a N |
Taking the lim sup on both sides as n approaches infinity (N is fixed) we obtain, using the result on the n-th Root Sequence: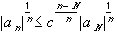
lim sup | a n | 1/nHence, the sequence satisfies to root test, and therefore the series converges absolutely.c < 1
The proof of divergence is left as an exercise.

 Interactive Real Analysis
Interactive Real Analysis