Theorem 4.2.9: Geometric Series
Examples 4.2.10:
Investigate the convergence properties of the following series:
The first series
- What is the actual limit of the sum
.gif) ?
?
- What is the actual limit of the sum
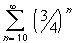 ?
?
- Does the sum
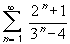 converge ?
converge ?
.gif) seems to be a geometric series with a = 1/2.
seems to be a geometric series with a = 1/2.
However, the index n starts at n = 1, whereas for the geometric series it starts at n = 0. While that does not influence the convergence behavior, it does change the actual limit of the series. In fact, the we have that:
1 +by the geometric series test, so that= 1 / (1 - 1/2)
The second series= 1 / (1 - 1/2) - 1 = 1.
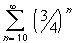 is again similar to the geometric series, except for the index,
which is supposed to start at 0. This does not influence
convergence (or divergence) but it does change the actual value
of the series.
is again similar to the geometric series, except for the index,
which is supposed to start at 0. This does not influence
convergence (or divergence) but it does change the actual value
of the series.
While
we have for our series:= 1 / (1 - 3/4) = 4
which is the answer to the above infinite series.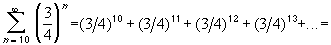
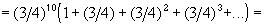
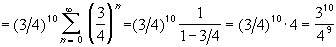
For the last series
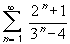 we will use the limit comparison test, together with the
geometric series test.
we will use the limit comparison test, together with the
geometric series test.
First note that
Therefore, by the limit comparison test, the series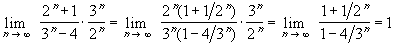
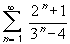 and
and
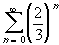 have the
same convergence behavior. But by the geometric series test,
the second series converges, so that by the limit comparison
test the first one also converges.
have the
same convergence behavior. But by the geometric series test,
the second series converges, so that by the limit comparison
test the first one also converges.
Note that we have established convergence of the series, but we do not know the actual limit. In fact, that limit is very difficult to determine.
 Interactive Real Analysis
Interactive Real Analysis