Cauchy Condensation Test
Examples 4.2.8:
Use the Cauchy Condensation criteria to answer the following
questions:
- In the sum
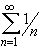 ,
list the terms
a 4, a k, and
a 2 k. Then show that
this series (called the harmonic series) diverges.
,
list the terms
a 4, a k, and
a 2 k. Then show that
this series (called the harmonic series) diverges.
- For which p does the series
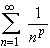 converge or diverge ?
converge or diverge ?
The sequence { 1/n } corresponds to the harmonic series. Therefore:
- a 4 = 1/4
- a k = 1/k
- a 2 k = 1 / 2 k
and the last series diverges by the Divergence test. Hence, the original series also diverges.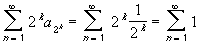
Next, we investigate the series
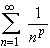 for various p:
for various p:
- If p < 0 then the sequence
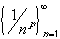 converges to infinity. Hence, the series diverges by the
Divergence Test.
converges to infinity. Hence, the series diverges by the
Divergence Test.
- If p > 0 then consider the series
The right hand series is now a Geometric Series, so that: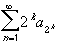 =
=
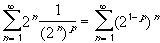
- if 0 < p
 1
then 2 1-p
1
then 2 1-p  1,
hence the right-hand series diverges
1,
hence the right-hand series diverges
- if 1 < p then 2 1-p < 1, hence the right-hand series converges
- if 0 < p
 Interactive Real Analysis
Interactive Real Analysis