4.1. Series and Convergence
Examples 4.1.5(b):
The series of absolute values is equal to
and this series converges, as shown before. It is in fact a special case of the geometric series..gif)
Hence, the series of absolute values converges, which by definition means that our series converges absolutely. Since absolute converge implies 'regular' convergence, the series also converges in its original form.
 Interactive Real Analysis
Interactive Real Analysis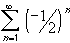 converges
absolutely.
converges
absolutely.