4.1. Series and Convergence
Examples 4.1.5(a):
The series
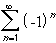
does
not converge.
Back
Consider the sequence of partial sums:
S n = -1 + 1 - 1 + 1 ... - 1 = -1
if
n is odd, and
S n = -1 + 1 - 1 + 1 ... - 1 + 1 = 0
if
n is even.
But then we have that
S n = -1 if n is odd and 0 if
n is even
or, in other words, the sequence of partial sums is the same as the
sequence
{ 1/2 ((-1)n-1)}
This sequence diverges, similar to the sequence
{(-1)n} we discussed previously. Hence, our sequence of partial sums - while bounded - does not converge and therefore the series is divergent.
 Interactive Real Analysis
Interactive Real Analysis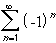 does
not converge.
does
not converge.