2.1. Countable Infinity
Proposition 2.1.6: Combining Countable Sets
- Every subset of a countable set is again countable (or finite).
- The set of all ordered pairs of positive integers is countable.
- The countable union of countable sets is countable
- The finite cross product of countable sets is countable.
Proof:
The first statement seems obvious. Nonetheless, it needs to be proved - as an exercise.To prove the second statement, we list all ordered pairs as follows:
(1,1) (1,2) (1,3) (1,4) ...
(2,1) (2,2) (2,3) (2,4) ...
(3,1) (3,2) (3,3) (3,4) ...
(4,1) (4,2) (4,3) (4,4) ...
... ... ... ... ...
Next, we have do devise a method for counting these elements in order to
enumerate all pairs. Here is one possible solution:
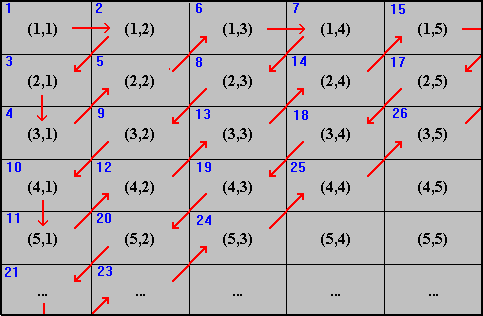
Diagonalized Counting of N x N
Since we are able to enumerate all elements in the above table, the set must be countable.
The proof of the next statement - that the countable union of countable sets is again countable - is very similar. Try to duplicate the above proof by writing down the elements from all sets in a table similar to the above table. The details are left as another exercise.
Finally, we need to prove the last statement: Suppose S(1), S(2), S(3), ..., S(n) are all countable. Then the cross product of those sets is defined to be
S := {(x(1), x(2), ..., x(n)) : x(j)If there were only two such sets, then the proof is exactly the same as the proof of the first statement. If there are more than two sets, we can group them. That is, considerS(j) for all j = 1, 2, ..., n}
S(1) x S(2) x S(3) x ... x S(n) = ( S(1) x (S2) ) x S(3) x ... x S(n)The first cross product is countable, because its a cross product of two countable sets. Then consider
S(1) x S(2) x S(3) x ... x S(n) = ( ( S(1) x (S2) ) x S(3) ) x ... x S(n)The cross product ((S(1) x (S2)) x S(3)) is countable, because it can be considered again as the cross product of only two sets, each of which is countable. Clearly we can continue in this fashion, and since there are only finitely many sets, we will have proved the third statement.

 Interactive Real Analysis
Interactive Real Analysis