2.4. The Real Number System
Examples 2.4.3(b):
Consider the set of rational numbers {1, 1.4, 1.41, 1.414, 1.4142, ...}
converging to the square root of 2. If all we knew were rational numbers,
this set would have no supremum. If we allow real numbers, there is
a unique supremem.
If we consider the universe to consist only of rational numbers, then
this set does not have a least upper bound.
- No number bigger than
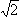 is the least upper bound (although each of these numbers is an upper bound),
because if x was that least upper bound, then we can find a rational
number between
is the least upper bound (although each of these numbers is an upper bound),
because if x was that least upper bound, then we can find a rational
number between 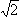 and
x. That rational number would then be an upper bound smaller than
x, which is a contradiction.
and
x. That rational number would then be an upper bound smaller than
x, which is a contradiction.
- No number less than
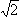 is the least upper bound, because if x was that least upper bound,
there is some element of the set between x and
is the least upper bound, because if x was that least upper bound,
there is some element of the set between x and
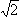 . But then x is not
an upper bound, which is a contradiction.
. But then x is not
an upper bound, which is a contradiction.
If we consider this set as a subset of the real numbers, then the least
upper bound of this set is 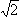 .
.
 Interactive Real Analysis
Interactive Real Analysis