2.3. The Principle of Induction
Examples 2.3.4(a):
Use induction to prove the following statements:
1. The sum of the first n positive integers is n (n+1) / 2
- The sum of the first n positive integers is n (n+1) / 2.
- If a, b > 0, then
(a + b)n
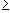 an + bn for any positive
integer n.
an + bn for any positive
integer n.
To use induction, we have to proceed in fours steps.
- Property Q(n):
- 1 + 2 + 3 + ... + n = n (n+1) / 2
- Check Q(1):
- 1 = 1 * 2 / 2, which is true.
- Assume Q(n) is true:
- Assume that 1 + 2 + 3 + ... + n = n (n+1) / 2.
- Check Q(n+1):
-
1 + 2 + 3 + ... + n + n + 1 =
Hence, Q(n+1) is true under the assumption that Q(n) is true.
= (1 + 2 + 3 + ... + n) + (n + 1) =
= n (n+1) / 2 + (n+1) =
= n (n+1) / 2 + (2n + 2) / 2 =
= (n+1)(n+2) / 2
2. If a, b > 0, then
(a + b)n 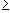 an + bn
for any positive integer n.
an + bn
for any positive integer n.
Using an induction proof, we have to proceed in four steps:
- Property Q(n):
- (a + b)n
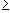 an + bn
if a, b > 0
an + bn
if a, b > 0
- Check Q(1):
- (a + b)
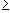 a + b, which is true.
a + b, which is true.
- Assume Q(n) is true:
- Assume that
(a + b)n
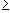 an + bn
an + bn
- Check Q(n+1):
-
(a + b)n + 1 = (a + b)n (a + b)
because a, b > 0. Hence, Q(n+1) is true under the assumption that Q(n) is true.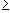 (an + bn) (a + b) =
(an + bn) (a + b) =
= an + 1 + an b + a bn + bn + 1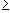 an + 1 + bn + 1
an + 1 + bn + 1
 Interactive Real Analysis
Interactive Real Analysis