2.1. Countable Infinity

Example 2.1.8: Hilbert's Hotel

Imagine two hotels in Boston, Massachusetts; the Holiday Inn, which has three hundred rooms and Hilbert's Hotel, which contains a countable infinite number of rooms. The New York Yankees are leaving town after defeating the Red Sox, again! However, their tour bus breaks down and they are forced to get off the bus and stay overnight in Boston. The Yankees, excluding their pitching coach, decide to walk to the Holiday Inn only to find that all three hundred rooms are already occupied. At the same time the pitching coach decides to walk over to Hilbert's Hotel because he heard it was a nicer hotel. When the pitching coach arrives at Hilbert's Hotel, he discovers that all of the rooms are taken as well. However, the manager of the hotel, a Mr. Hilbert, is an extremely big Yankee fan and promises to do his best.

One more Person

If all of the rooms are occupied, how is the manager of Hilbert's Hotel going to find a room for the pitching coach?

Since the hotel has an infinite number of rooms, the manager can move every guest over by one room. Now the first room is empty, nobody had to leave, and the hotel can accommodate the the pitching coach without problems.

In other words, the guest in room 1 moves to room 2, the guest in room 2 moves to room 3, and so on. Now room 1 is available for the pitching coach even though nobody left.

Mathematically speaking, the guest in room n moves to room n+1 for all n and the new guest moves into room 1. Or, more precicely, the function f: N 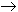N\{1} with f(n) = n+1 is a bijection, which means that card(N) = card(N\{1}), or in Hilbert's Hotel situation that everyone can move over by one yet everyone will continue to have their own room.

Two more People

After the pitching coach settles into his room, he calls his two best friends, the right fielder and the shortstop, to tell them to come over to Hilbert's Hotel for a room. When they arrive at Hilbert's Hotel the manager informs them that all the rooms are still occupied, but he can find accommodations for two more people (for an extra price, of course -:).

If all of the rooms are still occupied, how can the manager of Hilbert's Hotel find room for two more players?

Simple, thinks the manager, what worked once will work twice. He moves the pitching coach from room 1 to room 3, the guest in room 2 to room 4, the guest in room 3 to room 5, the guest in room 4 to room 6, and so on. Each guest tells the one in the room he/she is about to move into to move up by 2 rooms. At the end room 1 and 2 are available for the right fielder and the shortstop.

In other words, the guest in room n moves to room n+2 for all n.

Housing the Team

The Yankees soon find out that Hilbert's Hotel is accommodating some of the members of their team and the manager of the hotel finds himself trying to find rooms for the rest of the members. There were fifty-eight people that need to find a room and still none of the guests should checked out of the hotel. The manager of the hotel says not to worry because he could find rooms for the entire team.

If every room is occupied, how can the manager find enough rooms for the entire team of 58?

By now the manager has lots of experience. Since there were fifty-eight Yankees that still need to find a room, the manager moves the shortstop from room 1 over to room 59, the right fielder from room 2 to room 60, the pitching coach from room 3 to room 61, and so on. Each guest moves up by 58 rooms, which naturally creates fifty-eight available rooms - all of the Yankees move in happily.

Of course you guessed that we could also say that the guest in room n moves to room n+58 for all n.

The Fans are coming

Throughout the night, rumors spread that the Yankees are staying in Hilbert's Hotel. Many fans from the surrounding area travel to Hilbert's Hotel to book a room. When Hilbert looks outside his hotel, he sees a never-ending line of people that wish to stay for the night. But Hilbert wonders how he could find rooms for a countable infinite number of guests ... then he looks outside the hotel again and reassures the people waiting in line that everyone will soon have a room for the night.

How could the manager of the hotel accommodate a countable infinite number of guests?

This is a little trickier. After some thought Hilbert, our crafty Hotel manager, decides to move every one of his guests into the room with room number twice the original. For example, the guest staying in room 1 moves to room 2, the guest in room 2 moves to room 4, the guest in room 3 moved to room 6 and so on. This will eventually leave all guests in even-numbered rooms only and the odd-numbered rooms have become availability! Since we know that the set of all odd numbers is countable infinite, Hilbert just found room for the countable infinite number of guests by moving them into the odd-numbered rooms.

What would this mean phrasing in in terms of "room n" and "cardinality of sets"?

This version of Hilbert's Hotel has been created by Jillian Gaglione, a former Seton Hall student and avid Yankee (a New York baseball team) fan - with apologies to any Red Sox (a Boston baseball team) fan.
Next | Previous | Glossary | Map