2.2. Uncountable Infinity
Example 2.2.7: A Hierarchy of Infinity - Cardinal Numbers
When dealing with cardinal numbers, one can establish the following rules and
definitions:
- Definition of a cardinal number
- Comparing cardinal numbers
- The power of the continuum and the cardinality aleph null
- Addition of two cardinal numbers
1. Definition of Cardinal Number
- Two sets A and B are called equivalent if there exists a bijection between A and B. The two sets are said to have the same cardinality, or power.
- The cardinality of a set A is denoted by card(A).
- The cardinal numbers of two sets are equal if the sets are equivalent.
2. Comparing Cardinal Numbers
- A cardinal number c is less than or equal to another cardinal
number d if there exist two sets A and B with
card(A) = c and card(B) = d and
card(A)
 card(B)
card(B)
3. Special Cardinalities
The cardinality of the real numbers is called the cardinality (or power) of the continuum, and is denoted by- c = card(R).
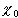 = card(N)
= card(N)
4. Adding Cardinal Numbers
Let c and d be two cardinal numbers and take sets A and B with card(A) = c and card(B) = d. Define the sets- A' = {(a, 0) : a
 A}
A}
- B' = {(b, 1) : b
 B}
B}
- c + d = card(A'
 B')
B')
Example:
Let A = {1,2,3} and B = {1,2}. Then card(A) = 3 and card(B) = 2. However,- card(A
 B) = 3
B) = 3
 B = {1,2,3}.
Using the above definition, we get:
B = {1,2,3}.
Using the above definition, we get:
- A' = { (1,0), (2,0), (3,0)}
- B' = { (1,1), (2,1) }
- A'
 B' =
{(1,0), (2,0), (3,0), (1,1), (2,1)}
B' =
{(1,0), (2,0), (3,0), (1,1), (2,1)}
- card(A'
 B')
= 5 = card(A) + card(B)
B')
= 5 = card(A) + card(B)
 Interactive Real Analysis
Interactive Real Analysis