1.1. Introduction

Ex 1.1.4 (c): Properties of the Imaginary Unit

Use the definition of i to solve z2 + 1 = 0 and z4 + 1 = 0

Well, the first equation is easy to solve:

z2 + 1 = 0 is equivalent to z2 = -1
Taking the square root on both sides
|z| = or z = + = i and z = - = -i

by the definition of i. Note that I do get 2 solutions for a second-degree polynomial.

The second equation is harder. We want to know those z such that

z4 + 1 = 0
But that is equivalent to z4 = -1 or z2 = i. Letting z = x + iy, this yields (x + i y)2 = i. Separating the real and imaginary parts, we get the system of equations:
x2 - y2 = 0
2xy = 1
But that (non-linear) system of equations is easy to solve:
x = 1/
y = 1/
Thus, we have four solutions to our fourth degree polynomial:
z = 1/(1 + i),
z = 1/(1 - i),
z = 1/(-1 + i),and
z = 1/(-1 - i)
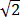
Please make sure to verify that each of these 4 answers, when raised to the 4th power, gives you -1. Note that we jumped the gun a little by writing z = x + i y. Technically, we still need to introduce the complex numbers, which we will do soon.
Next | Previous | Glossary | Map