1.1. Introduction
Ex 1.1.1: Properties of number systems
- a natural number without an additive inverse
- an integer without a multiplicative inverse
- a sequence of rational numbers that converges but the limit is not rational
1. That's simple, since no natural number has an additive inverse. Take the number 42, for example. To find its additive inverse, I have to find a number x such that
42 + x = 0since 0 is the additive identity. Clearly,x=-42, but that's not a natural number. So there ...
2. Again, simple: 42, for example, has no multiplicative inverse in the integers. This time we are looking for a number such that
42 x = 1because 1 is the multiplicative identity. Clearly, x = 1/42 which is not an integer.
3. That's a more interesting example. Take the limit of the recursively defined sequence
x0 = 2It can be shown that this sequence is bounded and monotone, so it must have a limit, and once you know that there is a limit, it is easy to show that the limit is indeed
xn+1 = 1/2 (xn + 2/xn)
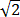 .
But
.
But 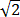 is not a rational number.
is not a rational number.
Alternatively, take the sequence of rational appromations to the square root of 2, i.e.
{1, 1.4, 1.41, 1.414, 1.4142, ...}. That sequence is a sequence of rational numbers that converges to a non-rational limit.
But strictly speaking, this argument involves some hand-waiving: what is the definition of that sequence, exactly? And how
exactly do you prove that the limit of this sequence really is 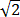 .
.
 Interactive Complex Analysis
Interactive Complex Analysis