back | next
1.4 Variables and Distributions
When we are looking at a particular population, selecting samples to make inferences, we need to record our observations or the characteristics of the data we are studying.
A variable is the term used to record a particular characteristic of the population we are studying.
For example, if our population consists of pictures taken from Mars, we might use the following variables to capture various characteristics of our population:
- quality of a picture
- title of a picture
- latitude and longitude of the center of a picture
- date a picture was taken
Categorical Variables are variables that have a limited number of distinct values or categories. They are sometimes called discrete variables.
Numeric Variables refer to characteristics that have a numeric values. They are usually continuous variables, i.e. all values in an interval are possible.
Categorical variables again split up into two groups, ordinal and nominal variables:
Ordinal variables represent categories with some intrinsic order (e.g., low, medium, high; strongly agree, agree, disagree, strongly disagree). Ordinal variables could consist of numeric values that represent distinct categories (e.g., 1=low, 2=medium, 3=high). To best remember this type of variable, think of "ordinal" containing the word "order".
Nominal variables represent categories with no intrinsic order (e.g., job category or company division). Nominal variables could also consist of numeric values that represent distinct categories (e.g., 1=Male, 2=Female).
It is usually not difficult to decide whether a variable is categorical (discrete) or numerical (continues).
Example: An experiment is conducted to test whether a particular drug will successfully lower the blood pressure of people. The data collected consists of the sex of each patient, the blood pressure measured, and the date the measurement took place. The experiment is conducted three times, once before the patient was treated, once one hour after administrating the drug, and again 2 days after administrating the drug. What variables comprise this experiment?
The characteristics measured in the experiment are the patient's sex, blood pressure, and the date. The sex is a nominal variable, the blood pressure is numeric, and the date is ordinal. The fact that the experiment is repeated does not change the number of variables recorded, each time 3 variables are recorded.
Note that recording these three variables only would not enable a successful data analysis. It seems likely that in order to test the drug's effectiveness you need to correlate the measurements taken on different dates with particular patients. In other words, you want to know what the blood pressure for each patient was each time you took it. Thus, you should introduce at least one more variable into your experiment, such as a patient ID (which is a nominal variable, even though the ID could be a number).
Example: Consider the following survey, given a random sample of Seton Hall University students:
Q1: What is your status: [ ] Freshmen [ ] Sophomore [ ] Junior [ ] Senior [ ] Graduate Student
Q2: What is your major: __________________
Q3: What is your age: ___________________
Q4: How often do you use the following support services?
daily few times
per weekfew times
per monthfew times
per yearnever Academic Advisement The Career Center Dining Services Health Services Counseling Services Recreation Center PC Support Services Campus Ministry Q5. The following student support services are effective.
Note: 1 =Strongly Agree, 2 =Agree, 3 =Neutral, 4 =Disagree, 5 =Strongly Disagree, -1 =Not Applicable
1 2 3 4 5 -1 Academic Advisement The Career Center Dining Services Health Services Counseling Services Recreation Center PC Support Services Campus Ministry The survey consists of a total of 19 variables, as follows: Q1 is an ordinal variable, Q2 is nominal, and Q3 is numeric. Q4 consists of 8 variables (corresponding to 8 rows of the table), all being ordinal, and Q5 again consists of 8 ordinal variables. Note in particular that the 8 variables in questions 5 are not numeric. The numbers are simply codes for particular categories.
When the results of a survey or an experiment are recorded, the results usually vary. Most or all outcomes for each variable occur, and they usually occur with different frequencies. Recognizing patterns in the frequencies of outcomes is in fact one of the goals of statistics.
The distribution of a variable refers to the set of all possible values of the variable and the associated frequencies or probabilities.
Sometimes variables are distributed so that all outcomes are equally, or nearly equally likely. Other variables show results that "cluster" around one (or more) particular values.
A heterogeneous distribution is a distribution of values of a variable where all outcomes are nearly equally likely.
A homogeneous distribution is a distribution of values of a variable that cluster around one or more values, while other values are occurring with very low frequencies or probabilities.
Example: Suppose you are conducting a survey that tries to determine whether woman are typically smaller than men. Thus, your survey, given to 100 randomly selected people, asks for the respondent's sex and height. Do you anticipate homogeneous or heterogeneous distributions from these variables?
Since approximately half of all people are male and half are female, and the survey was given to 1000 randomly selected participants, there should be approximately the same number of men and women queried. Thus, the variable sex should have a heterogeneous distribution, both values are just about equally likely. The second variable, height, however, will likely cluster around one or two most frequent values. Or conversely, few people are really short (4 feet or less) or really tall (7 feet or more), so this variable should be homogenously distributed.
Example: Suppose a company issues sales reports for two years, 2004 and 2005, as shown in the table and picture below. We can consider this report to consist of two variables (v_2004 and v_2005, say), each one having 4 values (for North, South, East, and West, respectively). Are the distributions of values hetero- or homogeneous?
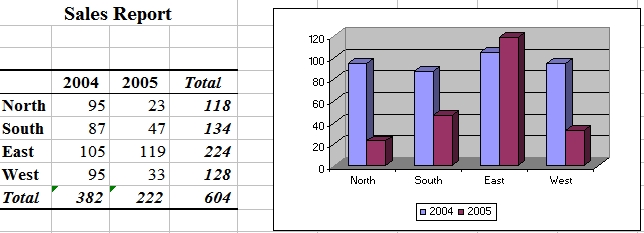
The values for the 2004 variable (v_2004 if you like) are pretty close to each other. In the chart you can see that all blue bars are approximatley of equal height. If I would look at the original figures, I would find an (about) equal amount of sales for North, South, East, and West, no region would stick out, particularly. Thus, each region is equally likely in terms of number of sales - the distribution is heterogeneous (if I checked where an individual, randomly selected, came from, each region would be approximately equally likely).
The values for the 2005 variable (v_2005 in our terminology) differ widely. In the chart the red bars are of different heights, with "East" being by far the highest. If I would look at the original figures, I would find that most sales were made in the East. Thus, a sale from the East is much more likely than from any other region - the distribution is homogeneous (if I checked where an individual, randomly selected, came from, she would most likely come from the east).
Discussion Topic: Which type of variable (ordinal, nominal, or numeric) you think will be most useful for statistical analysis? Which type of variable you think is usually present in a surveys given to groups of people? Look at survey results from newspapers or online and report the variables and their categories.
 MathCS.org - Statistics
MathCS.org - Statistics