5. Topology
5.1. Open and Closed Sets
In the previous chapters we dealt with collections of points: sequences and series. Each
time, the collection of points was either finite or countable and the most important
property of a point, in a sense, was its location in some coordinate or number system.
Now will deal with points, or more precisely with sets of points, in a more abstract setting.
The location of points relative to each other will be more important than their absolute
location, or size, in a coordinate system. Therefore, concepts such as addition and
multiplication will not work anymore, and we will have to start, in a sense, at the
beginning again.
All of the previous sections were, in effect, based on the natural numbers. Those numbers
were postulated as existing and all other properties - including other number systems -
were deduced from those numbers and a few principles of logic.
We will now proceed in a similar way: first, we need to define the basic objects we want
to deal with, together with their most elementary properties. Then we will develop a
theory of those objects and called it topology.
| Examples 5.1.2: |
| |
- Which of the following sets are open, closed, both, or neither ?
 The intervals (-3, 3), [4, 7], (-4, 5], (0,
The intervals (-3, 3), [4, 7], (-4, 5], (0,  )
and [0, )
and [0,  ) )
 The sets R (the whole real line) and 0 (the empty set)
The sets R (the whole real line) and 0 (the empty set)
 The set {1, 1/2, 1/3, 1/4, 1/5, ...} and {1, 1/2, 1/3, 1/4, ...}
The set {1, 1/2, 1/3, 1/4, 1/5, ...} and {1, 1/2, 1/3, 1/4, ...}
 {0} {0}
|
It is fairly clear that when combining two open sets (either via union or intersection) the
resulting set is again open, and the same statement should be true for closed sets. What
about combining infinitely many sets ?
How complicated can an open or closed set really be ? The basic open (or closed) sets in
the real line are the intervals, and they are certainly not complicated. As it will turn out,
open sets in the real line are generally easy, while closed sets can be very complicated.
The worst-case scenario for the open sets, in fact, will be given in the next result, and we
will concentrate on closed sets for much of the rest of this chapter.
Next we need to establish some relationship between topology and our previous studies, in
particular sequences of real numbers. We shall need the following definitions:
| Definition 5.1.5: Boundary, Accumulation, Interior, and Isolated Points |
| |
Let S be an arbitrary set in the real line R.
- A point b
 R is called
boundary point of S if every non-empty neighborhood of b
intersects S and the complement of S. The set of all boundary
points of S is called the boundary of S, denoted by
bd(S). R is called
boundary point of S if every non-empty neighborhood of b
intersects S and the complement of S. The set of all boundary
points of S is called the boundary of S, denoted by
bd(S).
- A point s
 S is called
interior point of S if there exists a neighborhood of
S completely contained in S. The set of all interior points
of S is called the interior, denoted by int(S). S is called
interior point of S if there exists a neighborhood of
S completely contained in S. The set of all interior points
of S is called the interior, denoted by int(S).
- A point t
 S is called
isolated point of S if there exists a neighborhood U of
t such that U S is called
isolated point of S if there exists a neighborhood U of
t such that U  S = {t}. S = {t}.
- A point r
 S is called
accumulation point, if every neighborhood of r contains infinitely
many distinct points of S. S is called
accumulation point, if every neighborhood of r contains infinitely
many distinct points of S.
|
| Examples 5.1.6: |
| |
 What is the boundary and the interior of (0, 4), [-1, 2], R,
and O ? Which points are isolated and accumulation points, if any ?
What is the boundary and the interior of (0, 4), [-1, 2], R,
and O ? Which points are isolated and accumulation points, if any ?
 Find the boundary, interior, isolated and accumulation points, if any, for the
set {1, 1/2, 1/3, ... }
Find the boundary, interior, isolated and accumulation points, if any, for the
set {1, 1/2, 1/3, ... }  {0} {0}
|
Here are some results that relate these various definitions with each other.
Finally, here is a theorem that relates these topological concepts with our previous notion
of sequences.
 R is
called open, if for each x
R is
called open, if for each x  U
there exists an
U
there exists an  > 0 such that the interval
( x -
> 0 such that the interval
( x -  , x +
, x +  )
is contained in U. Such an interval is often called an
)
is contained in U. Such an interval is often called an
 - neighborhood of x, or simply
a neighborhood of x.
- neighborhood of x, or simply
a neighborhood of x.
 R be an arbitrary open
set. Then there are countably many pairwise disjoint open intervals
Un such that U =
R be an arbitrary open
set. Then there are countably many pairwise disjoint open intervals
Un such that U =
 Un
Un
 Interactive Real Analysis
Interactive Real Analysis )
and [0,
)
and [0,  S = {t}.
S = {t}.
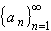 is any sequence in S, then
there exists a subsequence
is any sequence in S, then
there exists a subsequence 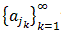 of
of