4.3. Special Series
Theorem 4.2.9: Geometric Series
Let a be any real number. Then the series
.gif) is called Geometric Series.
is called Geometric Series.
.gif) is called Geometric Series.
is called Geometric Series.
- if | a | < 1 the geometric series converges
- if | a |
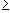 1
the geometric series diverges
1
the geometric series diverges
=
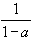
Note that the index for the geometric series starts at 0. This is not important for the convergence behavior, but it is important for the resulting limit.
| Examples 4.2.10: | |
| |
The proof consists of a nice trick. Consider the partial sum S N and multiply it by a:
- S N = 1 + a + a 2 + a 3 + ... + a N
- a S N = a + a 2 + a 3 + ... + a N+1
 Interactive Real Analysis
Interactive Real Analysis.gif) ?
?
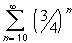 ?
?
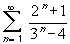 converge ?
(Here the
converge ?
(Here the