4.1. Series and Convergence
Theorem 4.1.8: Algebra on Series
Let 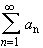 and
and
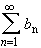 be two absolutely convergent series. Then:
be two absolutely convergent series. Then:
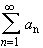 and
and
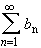 be two absolutely convergent series. Then:
be two absolutely convergent series. Then:
- The sum of the two series is again absolutely convergent. Its limit is the sum of the limit of the two series.
- The difference of the two series is again absolutely convergent. Its limit is the difference of the limit of the two series.
- The product of the two series is again absolutely convergent. Its limit is the product of the limit of the two series (Cauchy Product ).
Proof:
The proof of the first statement is a simple application of the triangle inequality. LetAn = |a1| + |a2| + ... + |an|and
Bn = |b1| + |b2| + ... + |bn|Assume that An converges to A and Bn converges to B. Then
Sn = |a1 + b1| + |a2 + b2| + ... + |an + bn|Therefore the sequence {Sn} is bounded above by A + B. The sequence is also monotone increasing so that it must converge to some limit. To find the limit, note that
|a1| + |a2| + ... + |an| + |b1| + |b2| + ... + |bn|
A + B
| (a1 + b1) + (a2 + b2) + ... (an + bn) - (A + B)|if n is big enough. Therefore the sequence {Sn} converges to A + B, as required.
| a1 + a2 + ... + an - A | + | b1 + b2 + ... + bn - B |
</ 2 +
/ 2
The proof for the difference of sums is similar. The proof for the Cauchy product, on the other hand, is much more complicated and will be given in the statement on the Cauchy Product.
 Interactive Real Analysis
Interactive Real Analysis